Pushdown Automata and Context-free Grammar

Pushdown Automata

下推自动机可以看作是 NFA 加入栈后的拓展版本。与 NFA 相比，PDA 的定义中多了一个“栈”的概念，一个 PDA 由六元组 $(Q, \Sigma, \Gamma, \delta, q_0, F)$ 组成。其中：

• $Q, \Sigma, q_0, F$​ 与 NFA 的定义完全一致，它们分别表示状态，字符集，起始节点，接受节点集。
• $\Gamma$ 是栈字符集，它规定了栈中的每个元素可能是什么。我们常常通过往栈中压入或者弹出一个 $ 来确保当前栈是空的。
• $\delta$ 同样是转移函数，但它与 NFA 的区别是引入了栈的状态。$\delta$ 函数接受当前状态、当前栈顶以及一个字符（当然，可以是空串 $\epsilon$），它的输出是一个目标节点以及对当前栈的操作（不从栈顶读字符并压入一个字符、弹出一个字符、更改栈顶字符或者保持栈不动）。更为形式化地说，$\delta$ 的定义是 $Q\times \Sigma_{\epsilon}\times \Gamma_{\epsilon}\to Q\times \Gamma_{\epsilon}$​（输入栈顶即将被替换的那个字符，输出新的栈顶）。

我们称字符串 $w$ 可以被这个 PDA 识别，当且仅当存在一系列状态 $s_0, \cdots, s_m$ 以及栈构成的字符串 $t_0, \cdots, t_m$，使得

• $s_0 = q_0, t_0=\epsilon$：一开始在起始节点；栈是空的
• 对于每个 $i= 0, 1, \cdots, m-1$，存在 $a, b\in \Gamma_{\epsilon}$，以及 $r\in \Gamma^*$ 使得 $t_i=ar, t_{i +1}=br$。且 $(s_{i+1}, b)\in\delta(s_i, w_{i+1},a)$。注意 $a, b$ 可以是空的，这就完成了对栈的操作。
• $s_m\in F$​，即必须在接受节点结束。

Context-free Grammar

所谓上下文无关语法就是“只能通过一定规则生成”的语法。它的形式化定义由四元组 $(V,\Sigma,R,S)$ 构成，其中：

• $V$ 表示变量集合。所谓“变量”，在这里指的是满足特定规则的某个字符串（可以看作里面存的就是一个字符串，但是必须满足某些限制）
• $\Sigma$ 表示字符集合，它规定了字符串中可能出现的所有字符。
• $R$ 是规则集合，它规定了 $V$ 中变量必须服从的规则，每条规则会将一个 $V$ 中的变量和一个包含变量以及字符的字符串结合起来。或者它也可以看作若干条“文本替换规则”，即每次将当前字符串中的一个变量替换为另一个字符串（可能包含变量）。
• $S\in V$ 表示起始变量。

我们称字符串 $w$ 能被此语法生成，当且仅当从 $S$ 能导出字符串 $w$。举个例子，考虑下面的上下文无关语法：
$$
G=(\{S\}, \{a, b\}, R,S)\\\quad R: S\to aSb\ |\ SS\ |\ \epsilon
$$
它能生成 ab，abab，aabbab 等等字符串。

Corelation

事实上，下推自动机和上下文无关语法是等价的。即：任意下推自动机能表示的语言都能通过某种上下文无关语法生成，任意上下文无关语法都能对应一个下推自动机。证明由两个方向进行：

1. 任意上下文无关语法都对应一个下推自动机。
2. 任意下推自动机都对应一个上下文无关语法。

可以发现，1 是较容易证明的。构造自动机的思路是，先让自动机不接受任何输入，生成所有可能的字符串堆在栈里（即每一种在自动机上的走法结束后，栈中留下的都是一种可能的字符串）。然后自动机开始接受字符串，将其与当前栈顶比较，只有二者完全相同才弹出栈。

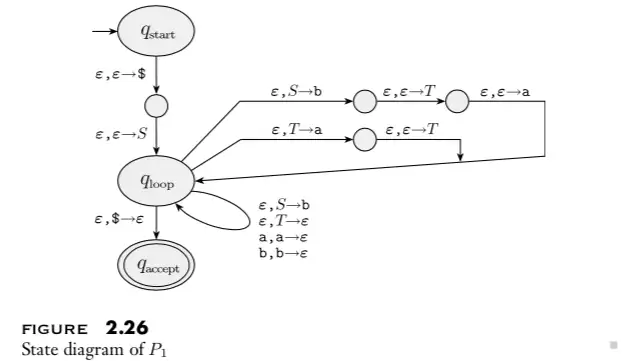
比如上面的那个例子，对于它我们可以构造出如下自动机：用 $x, y \to z$ 表示接受字符 $x$，取出栈顶并确认其为 $y$，向栈压入 $z$。

• 起始节点 $q_0$，向节点 $q_1$ 连边 $\epsilon, \epsilon\to \text{\$}$，意思是往当前栈中压入一个特殊字符用于判断栈是否为空。
• 节点 $q_1$ 向节点 $q_{loop}$ 连边 $\epsilon, \epsilon \to S$，这是因为起始字符是 $S$，意思是让当前字符串有一个字符 $S$。
• $q_{loop}$ 的连边有两种：
  1. 如果栈顶和接受字符串的第一个字符相同，那么弹出栈顶，对应向自己的连边 $a, a\to \epsilon $ 以及 $b, b\to \epsilon$。
  2. 应用一条规则。比如规则 $S\to aSb$，如果栈顶为 $S$，则弹出栈顶，并相继压入 b，$S$​，a。
• $q_{loop}$ 向接受节点 $q_{accept}$ 连边，弹出特殊字符用来确保当前栈为空。

下图是规则 $S\to aTb|b, T\to Ta|\epsilon$ 的例子。

接下来我们讨论关于 2 的证明。不妨假设这个自动机有 $k$ 个节点，我们生成 $k^2$ 个变量 $A_{pq}$，这里 $p,q$ 都是节点的编号，它用于表示所有从 $p$ 出发，并且出发时栈为空，能够到达 $q$ 且此时栈为空的字符串。那么，我们可以对其生成两种类型的规则。

1. 存在一个中间节点 $r$，使得自动机运行到节点 $r$ 时栈为空，那么根据定义可以构造出一条语法 $A_{pq}=A_{pr}A_{rq}$。
2. 如果存在字符串 $w$ 能从 $p$ 走到 $q$，拿出 $w$ 的第一个字符 $a$ 以及最后一个字符 $b$，并且记录下 $w$ 第一步走到的节点 $r$ 以及到达 $q$ 之前的节点 $s$，生成语法 $A_{pq}=aA_{rs}b$。由于 $\Sigma, Q$ 都是有限的，因此这样生成的规则也只有有限多条。

通过对字符串 $w$ 的长度 $|w|$ 归纳，可以很方便地证明任意能在这个自动机上跑的字符串都能被我们构造出的语法生成。

对上下文无关语法的 Pumping Lemma

Pumping Lemma

若 $A$ 是一种上下文无关语法，则存在一个数 $p$，使得对于 $A$ 能生成的任意字符串 $s$，如果 $|s| \ge p$，那么 $s$ 可以被划分为 $5$ 个部分 $uvxyz$，使得

对于任意的 $i\ge 0$，$uv^ixy^iz\in A$。

$vy$ 不为空。

$|vxy|\le p$。

只要 $s$ 足够长，那么生成出 $s$ 这个串对应的树形结构的深度就可以有保证。而这个深度一旦超过了点数，根据抽屉原理其中必然存在两个相同的变量（下图中的 $N$）。将深度更浅的 $N$ 对应的子树复制到深度更深的 $N$ 中，得到的串应当仍然满足上下文无关文法要求。