Simplex and Linprog
线性规划基础
线性规划指的是目标函数以及约束条件都是线性函数时的最优化问题。对于最一般的情况,我们可以用如下的形式刻画要解决的问题:
- 目标函数: $c(x_1, \cdots, x_n)=\sum_{j=1}^n c_j x_j$,我们想要最大化(或者最小化也可以)它,这里 $c_i$ 可正可负。
- 约束条件: $\sum_{j=1}^n a_{ij}x_j\le b_i$ (当然,$\ge$ 或者 $=$ 也是可以的,它们都可以用 $\le$ 表示)。有 $m$ 条约束条件($a$ 的下标就是这么来的)。
- 对于变量的非负性约束:有些 $x_i$ 可以随便取,但是有些 $x_i$ 不能小于 $0$。(其实规定所有变量必须不低于 $0$ 是等价的)
这个模型有些复杂,它可以被规约到一个难度完全相同,但是表达形式更简单的问题。我们称这种最简形式为标准型:
- 目标函数:$c(x_1, \cdots, x_n)=\sum_{j=1}^n c_jx_j$,我们想要最大化它。
- 约束条件:$\sum_{j=1}^n a_{ij}x_j=b_i$。(全部改成 $\le$ 则被称作松弛型线性规划)
- 对于变量的非负性约束:$\forall i, x_i\ge 0$。
之后将系数 $a_{ij}$ 合并为矩阵 $\mathbf A\in M_{m\times n}$,将目标函数的系数合并为列向量 $\mathbf c=(c_1, \cdots, c_n)^\top$
一些定义
- 可行解:和看起来的意思一样,指的是一组满足所有约束条件的解。
- 可行域:所有可行解组成的集合,它肯定是一个凸集。
- 最优解:让目标函数取到最值时对应的可行解。可能有多个。
闭上眼睛感受一下,这个线性规划问题的解看起来就会满足一些性质(后面会严格证明)
- $x_1, x_2, \cdots, x_n$ 中所有在目标函数中系数不为 $0$ 的变量构成了一个高维的空间,而可行域则在这个空间内一个较低维的子空间内。
- 如果把每条约束条件看成一个低维的子空间(比如二维空间内的直线),那么可行域的每个端点都是若干个这样的子空间的交点。
- 最优解一定可以在可行域的某一个端点取到。
- 可以利用爬山的方式一步一步想最优解靠近(每次从当前的顶点挪到一个与它相邻的,但是更优的顶点)
由此诞生了另一些定义
另一些定义
- 基本解:在顶点位置,但不一定满足非负性约束的解。
- 基本可行解:是基本解,并且满足非负性要求。
接下来我们讨论单纯形。首先让我们从一个例子开始。
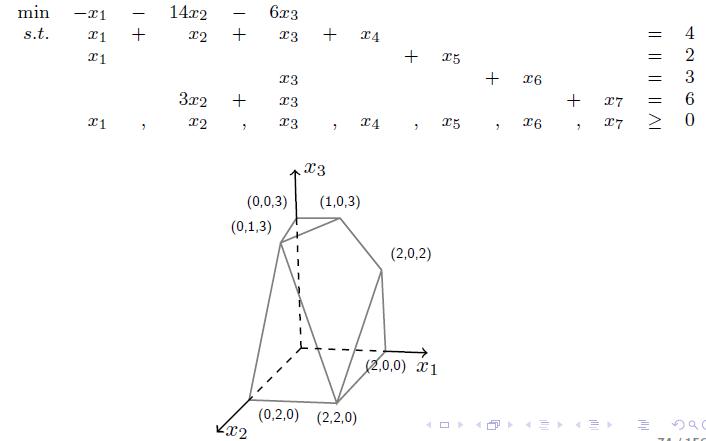
考虑 $x_1, x_2, x_3$ 所在的空间 $\mathbb R^3$,上面的约束条件可以看作在这个空间内圈定了一个区域。单纯形算法用基变量和非基变量两个概念将凸包的顶点和所有变量关联了起来:任意选定系数矩阵 $\mathbf A$ 极大的线性无关的若干列(对应的变量称为基变量),令没有选中的列对应的变量(称为非基变量)取值为 $0$,方程 $Ax=b$ 的解是唯一的,并且:
- 这个解一定对应到了凸包上的一个顶点。
- 凸包上的每个顶点都能这个样子解出来。
比如上面的例子,如果我们选定第 $2, 4, 5, 6$ 列,令 $x_1=x_3=x_7=0$,则可以解出唯一的解 $(0, 2, 0, 2, 2, 3, 0)$。它对应顶点 $(0, 2, 0)$。
为了说清楚 $\mathbf A$ 与整个凸包的关系 ,此时我们需要解决的问题是:
- 证明任意选择 $\mathbf A$ 的线性无关的若干列,直接令其余变量为 $0$,得到的解对应了一个顶点。
- 证明对于凸包的每一个顶点,都对应了 $\mathbf A$ 列向量的一个极大线性无关组。
一旦证明了这两点,我们就可以将不好处理的求顶点问题转化为便于计算的解方程问题。
Q:为啥得到的一定是一个顶点?
证明:如果得到的不是顶点,对于选定的 $\mathbf A$ 的基组成的矩阵 $\mathbf B$,方程 $\mathbf Bx=\mathbf b$ 得到的解 $\mathbf x=[x,0]^\top$ 可以被两个内部点对应的解 $\mathbf x_1, \mathbf x_2$ 线性表出。由于 $\mathbf x_1, \mathbf x_2$ 的非基变量取值非负,并且 $\mathbf x=\lambda_1\mathbf x_1+\lambda_2\mathbf x_2$,结合 $\mathbf x$ 的非基变量等于 $0$ 可以知道 $\mathbf x_1, \mathbf x_2$ 的非基变量也必须为 $0$。但是,由于 $\mathbf B$ 是满秩的,它的解唯一,也就是说 $\mathbf x_1, \mathbf x_2$ 的基变量取值完全相同,它们就是同一个点。因此解出的 $\mathbf x$ 一定是顶点。
Q:为啥每个顶点都解得出来?
更为严谨地说,我们想要说明的是这么一件事情:拿出凸包的一个顶点,随便解出一组解,如果在这个解中非 $0$,且在目标函数中系数为 $0$ 的变量对应的 $\mathbf A$ 的列向量线性无关(这当然是能做到的),那么整个解中非零元素对应的 $\mathbf A$ 的列向量也一定线性无关。
证明这个东西的意义是,证明凸包上的每个顶点都可以被解出来。
证明: 反证。如果整个解 $\mathbf x$ 中非零元素对应的 $\mathbf A$ 的列向量 $a_1, \cdots, a_k$ 线性相关,那么存在一组不全为 $0$ 的系数 $\lambda_1,\cdots, \lambda_k$ 使得 $\sum_{i=1}^k \lambda_i a_i=0$。根据条件可知必然有至少一个在目标函数中系数不为 $0$ 的变量,其对应的 $\lambda$ 也不为 $0$。对于除了 $a_1, \cdots, a_k$ 以外的其余列,令它们对应的 $\lambda$ 都是 $0$。这也就是说我们可以得到一个列向量 $\mathbf \lambda=(\lambda_1,\cdots, \lambda _n)^\top$,使得 $\mathbf A(\mathbf x+\lambda)=\mathbf b$。取一个很小很小的 $\theta$ 可以使得 $\mathbf A(\mathbf x+\pm\theta\lambda)=\mathbf b$ 成立且 $\mathbf x+ \pm \theta\lambda$ 的每个元素都不小于 $0$。这说明 $\mathbf x$ 对应的点可以被两个凸包内的点线性表示,它必不可能在凸包上。
单纯形
有了上面的结论,剩下的过程就比较简单了。单纯形就是把上面的所有东西全部揉了起来。不妨设 $\mathbf A$ 的秩是 $r$。
又一些定义
- 基:$\mathbf A$ 列向量的极大线性无关组。
- 基变量:基对应的变量。
- 非基变量:除了基变量之外的变量,我们认为它们一直都是 $0$。
- 基本解:指满足约束条件但不一定满足非负性条件,且非基变量全为 $0$ 的解。
- 基本可行解:在基本解的基础之上满足非负性条件的解。
- 可行基:基本可行解对应的基。
对于不需要初始化的松弛型线性规划(就是每个约束条件都是 $\le$),我们可以往里面添加 $m$ 个辅助变量 $x_{n+1}, \cdots, x_{n+m}$,将其变为标准型线性规划。因此这个时候的一个基本可行解就是 $(0, 0, \cdots, 0, b_1, \cdots, b_m)$。
转轴
接下来问题来到了如何找到相邻的更优秀的顶点以及如何挪过去。
继续考虑上面那个例子,假设我们已经选取了基变量 $x_1, x_4, x_6, x_7$,并且已经知道非基变量 $x_2, x_3, x_5 =0$。对于 $x_3$,列 $a_3$ 与 $a_1, a_4, a_6, a_7$ 线性相关,有
$$
a_3=0a_1+1a_4+1a_6+1a_7
$$
这也就是说 $0a_1+0a_2-1a_3+1a_4+0a_5+1a_6+1a_7=0$,将前面的系数提取为 $\lambda=(0, 0, -1, 1, 0, 1, 1)^\top$,有 $\forall \theta, \mathbf A(\mathbf x-\theta\lambda)=0$。我们可以通过选取合适的 $\theta>0$,使得某个已有的基变量在解 $\mathbf x-\theta\lambda $ 中变为 $0$,$x_3$ 的系数变为 $\theta$,这样就达到了“换基”的目的:我们将 $x_3$ 从非基变量换成了基变量,而将某一个基变量给换了出去。
考察换基前后目标函数的变化。一开始是 $\mathbf c^\top \mathbf x$,现在变为了 $\mathbf c^\top (\mathbf x-\theta\lambda)$,变化量为 $-\theta\mathbf c^\top\lambda$。对于每个非基变量(比如上面的 $a_3$),我们都可以计算出这个变化量。如果所有变化量都 $\le 0$,这说明我们已经找到了最优值,算法终止。否则根据爬山的策略,我们应该找到变化量最大的,进行一次换基操作。
$\theta$ 的选取需要满足 $\mathbf x - \theta\lambda$ 仍然全部非负。这就要求对于每个 $i\in \mathbf B, x_i-\theta\lambda_i\ge 0$。这里 $\mathbf B$ 指的是所有基变量的下标集合。如果 $\lambda_i<0$,那么此时不会出任何问题,可以发现直接令 $\theta=\min_{\lambda_i>0}\frac{x_i}{\lambda_i}$ 就是安全的。
接着考虑 $-\theta\mathbf c^\top\lambda$,在 $\lambda$ 中当前非基变量对应的值为 $-1$,其余位置只有基变量处的取值非 $0$。记行向量 $\bar{\mathbf c}$ 分别表示每个变量如果换入基变量,可以让答案增加多少(当然,对于当前的基变量,这个值为 $0$),由于 $\mathbf B^{-1}\mathbf A$ 刻画了此时 $\mathbf A$ 的每一列在基 $\mathbf B$ 下的坐标(其实就是 $\lambda$),结合上面的过程我们有 $\bar{\mathbf c}=\mathbf c^\top-\mathbf c_B^\top \mathbf B^{-1}\mathbf A$。这里 $\mathbf c_B^\top$ 表示只保留 $\mathbf c$ 中基变量对应的系数,其余系数填 $0$。

对偶线性规划
现在有这么一个线性规划:最小化 $7x_1+x_2+5x_3$,满足约束 $\begin{gathered}
x_1-x_2+3x_3\geq 10\\
5x_1+2x_2-x_3\geq 6\\
x_{1,2,3}\geq 0
\end{gathered}$。可以发现,这个线性规划相比于松弛形式的线性规划翻转了最大/最小化,同时原来的 $\le$ 也变成了 $\ge$。
聪明的你也许会有这样的想法:能不能直接把这些方程组合一下?比如,由于 $x_{1, 2, 3}\ge 0$,所以一定有 $7x_1+x_2+5x_3\ge x_1-x_2+3x_3\ge 10$。把这三个方程组合一下能否得到更紧的下界呢?
这等价于给这两个方程分配变量 $y_1, y_2$,需要满足 $\begin{gathered}y_1+5y_2\le 7 \\ -y_1+2y_2\le 1 \\ 3y_1-y_2\le 5\end{gathered}$,并且 $y_1, y_2$ 非负,同时最大化 $10y_1+6y_2$。这就是原线性规划的对偶问题。通过互松弛定理可以证明,原线性规划的最优解和对偶线性规划是相同的。由于对偶线性规划可以交换约束的数量和变量的数量,因此在解决某些问题的时候非常有用。
一些小练习
- $A,B$ 两个人在洞中发现了 $n$ 个石头,第 $i$ 个石头对于 $A$ 来说价值为 $A_i$,对于 $B$ 来说价值为 $B_i$。石头是可以切割的,并且价值与其体积成正比。现在$A,B$要分配这些石头,要求它们两个人最终得到的价值相同,问这个价值最大可以是多少
$$
n\leq 50, 0\leq A_i,B_i\leq 100
$$
源点和汇点唯一,其余每个点的流入流量必须等于流出流量,每条边有流量上界,问从源点到汇点的最大流。
最小费用流。即在最大流的基础之上,要求费用之和最小。每条边的单位流量有费用。
给一张 $n$ 个点的带权无向图,边 $u,v$ 的权值为 $w_{u,v}$,可以随意增加或者减少若干条边的边权,代价为边权的变化量。要求进行操作之后任意两点间直接相连的边的长度不超过两点之间的最短路,求最小代价。
给出三个长度为 $n$ 的数组 $a_i,b_i,c_i$,每次询问给出两个数 $s,t$,求一组非负实数 $x_i$,满足 $\sum_{i=1}^na_ix_i=s,\sum_{i=1}^nb_ix_i=t$,同时最大化 $\sum_{i=1}^nc_ix_i$。对于每组询问输出答案,或者判断无解。$n\le 10^5$,询问数不超过 $10^4$。
Simplex and Linprog